Background
"Geo-fencing" is the ability to define (and possibly enforce) a virtual 'fence' or perimeter, based on GPS locations, to determine whether a user is within the fence or outside it. It has come up a few times in the ODK Forum and elsewhere; eg geofencing-to-confirm-location, restrict-users-from-collecting-data-for-a-specific-area-geofencing. And there is even a longstanding feature request from 2010, which was 'solved' by exploiting accuraryThreshold to roughly define a circular 'fence'.
Another approximate solution, which may still be useful in some situations, is to define a rectangular fence based on minimum and maximum latitude and longitude, and then check the user's GPS coordinates lie within this range. This can all be accomplished using simple XForm calculations; see
adding-constraints-to-geopoint for a more detailed description of this approach.
A more sophisticated approach allows for an non-rectangular fence, and implements a point-in-polygon algorithm called the even-odd rule which uses using ray-tracing. An XForm-based solution of this for SurveyCTO is described here: https://medium.com/@jan_22556/geofencing-in-xlsform-odk-e892b94164ac , but requires pre-processing the fence and reading it into your form from an external CSV file. The even-odd algorithm allows for arbitrarily shaped fences, including concave polygons or even polygons with holes! However, there are non-trivial problems when the ray tracing happens to pass thru or near vertices of the polygon, which can result in points lying well outside the fence to be incorrectly identified inside, and vise versa.
ODK XForm Geofence
I wanted to try to see if I could come up with a standalone ODK XForm geofence solution that could take a regular ODK geoshape - either defined via a form control default or acquired from the user at runtime, and determine whether the user's geopoint location is inside or outside the fence. I chose to use a relatively simple point-in-polygon algorithm, initially one that works (only) for convex polygons because this is often sufficient (eg most real-world fences dont involve interior 'holes'). Specifically, it is an optimization of the winding number algorithm for convex polygons.
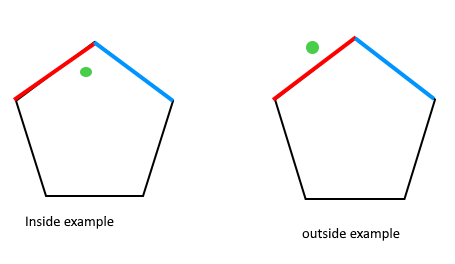
Basically, for an arbitrary (convex) polygon, the algorithm walks around each side of the polygon and checks which side of the line the desired point lies. If the point lies to the left of all the sides, or right of all the sides (depending on if you traverse the sides clockwise or counter-clockwise), then it is inside the polygon [first figure]. Otherwise, the point must lie outside the polygon [second figure]. One of the main advantages of the winding algorithm is that it doesn't suffer from the even-odd algorithm's vertex-ray intersection issue.
Geoshape
To begin, here is a map of the South Island of New Zealand, with a rough 5-sided bounding box geoshape - our 'fence'.
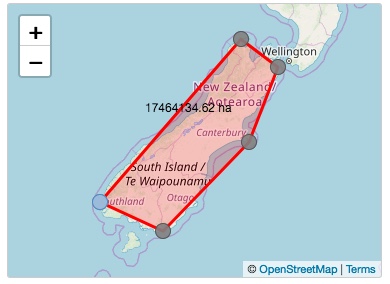
The first problem is extracting the latitude and longitude of every point of the polygon from the geoshape, which consists of 6 geopoints each separated by a ';' character. Each geopoint consists of an latitude, longitude, elevation and accuracy. The elevation and accuracy may be 0 (or 0.0), especially when selected from a map, but in general these can be real numbers and our solution must handle such. The above map produces:
Geopoints: #1 | #2 | #3 | #4 | #5 | #6
-------------------------+-------------------------+-------------------------+-------------------------+-------------------------+-------------------------
Geoshape: -45.773143 166.480072 0 0;-40.550261 172.650509 0 0;-41.481697 174.267668 0 0;-43.903698 173.031207 0 0;-46.654967 169.249557 0 0;-45.773143 166.480072 0 0
----------+----------+-+------------+----------+-+------------+----------+-+------------+----------+-+------------+----------+-+------------+----------+-+-
List: 1 2 3| 4 5 6| 7 8 9| 10 11 12| 13 14 15| 16 17 18 19
Lat1 Long1 | Lat2 Long2 | Lat3 Long3 | Lat4 Long4 | Lat5 Long5 | Lat6 Long6
Index: 0 1 2 3 4 5
If you instead view the geoshape as a space-separated list - ie the same sorta list that you can query using ODK's count-selected() and selected-at() functions... - then you can identify the index of each desired latitude and longitude (see above). Note, we are not interested in the altitude for geofencing.
Point-in-Polygon
Step 0: Before we start implementing the actual point-in-polygon algorithm, we extract our target point's latitude and longitude. Because a geopoint uses a space separator, this can be accomplished by:
targetLat = selected-at(${geopoint}, 0)
targetLong = selected-at(${geopoint}, 1)
Step 1: Next, using count-selected() we can calculate how many geopoints are in the geoshape fence. Each geopoint actually consists of only three list elements, because the accuracy value of the previous geopoint is prepended to the latitude of the latter, eg "0;-40.550261", except for the last geopoint. Hence
numpoints = (count-selected(${geoshape})-1) div 3)
or, equivalently
numsides = (count-selected(${geoshape})-1) div 3) - 1
Step 2: Now, we 'walk' around all the sides of the polygon by implementing a ODK repeat group, with a count of ${numsides}
begin_repeat | geopoints | repeat_count = ${numsides}
Step 3: Now within our repeat group, for each side of the polygon, we need to check whether the target point lies to the left or right of the line.
3a: In order to simplify the calculations, we calculate the 0-indexed position in the list for to the repeat iteration corresponding to the current side of the polygon:
index = position(..) - 1
3b: The first task is to extract the latitude and longitude of the two endpoints of the side. The longitude is easy because its value is always on its own in the list. Specifically, the longitude value of the first point for the current side is:
long = selected-at(${geoshape}, ${index}*3 + 1)
Similarly, the longitude for the second point (ie next index) is:
long2 = selected-at(${geoshape},(${index}+1)*3 + 1)
3c: Getting the latitude is a bit trickier, because in all cases except the first, the latitude value in the list is prepended with the accuracy of the previous geopoint, which might be "0;", "0.0;" or an arbitrary real number "0.12345;". Thankfully, someone recently added the substring-after() XPath function to ODK, which we can use to strip off this unwanted prefix... ![]()
latstr = selected-at(${geoshape}, ${index}*3 + 0)
lat = if(${index}=0, ${latstr}, substring-after(${latstr}, ';'))
The latitude for the second point (ie next index) will always need its prefix stripped, so it is simply:
latstr = selected-at(${geoshape}, (${index}+1)*3 + 0)
lat2 = substring-after(${latstr}, ';')
[BTW I added "... + 0" above to make it more obvious how we pick out specific values from the list based on the index. Obviously, adding 0 is mathematically redundant]
Step 4: Now we have the coordinates of both endpoints of the side, so we can finally determine which side of the line the target point lies, hurrah! Using a little geometry, this can be determined by checking the sign of the cross-product of vectors. From http://geomalgorithms.com/a01-_area.html:
// isLeft(): test if a point is Left|On|Right of an infinite 2D line.
// Input: three points P0, P1, and P2
// Return: >0 for P2 left of the line through P0 to P1
// =0 for P2 on the line
// <0 for P2 right of the line
inline int
isLeft( Point P0, Point P1, Point P2 )
{
return ( (P1.x - P0.x) * (P2.y - P0.y)
- (P2.x - P0.x) * (P1.y - P0.y) );
}
Basically, P2 is our target point, P0-P1 is our side, and P0-P2 is the second imaginary vector. The sign of the cross-product of vector P0-P1 and vector P0-P2 indicates which side of the line P0-P1 (fence side) that P2 (target) lies. In our XForm, this cross-product calculation looks like:
(${lat2}-${lat}) * (${targetLong}-${long})) - ((${targetLat} - ${lat}) * (${long2} - ${long})
And since we only need the sign:
isLeft = number(((${lat2}-${lat}) * (${targetLong}-${long})) - ((${targetLat} - ${lat}) * (${long2} - ${long})) > 0.0)
which will be 1 if left, or 0 if right.
Step 5: Our repeat group will perform this isLeft calculation for all the sides of our polygon. At the end, we just need to check if all the isLeft calculations returned 0, indicating the target point is right of all the sides (ie a clockwise polygon), or all 1, indicating the target is to the left (ie a counter-clockwise polygon). Both these cases indicate the point is wholly inside the polygon; anything else means it is outside. We can use the ODK sum() function to check all the calculation results from the repeat group:
sum = sum(${isleft})
inside = ${sum}=${numsides} or ${sum}=0
Ta-da!
Below I've attached an XLSForm which implements this geofence algorithm. The user first draws the fence on a map, and then selects a target point to check. A constraint on the geopoint will indicate whether the point is inside the fence. Load the form into https://opendatakit.org/xlsform/, have a play and let me know what you think! ![]()
geofence_v1.xls (23 KB)
Discussion
The above XLSForm works as desired under Enketo. However, I have noticed that when running it under Collect that the first time thru the form, the constraint on the geopoint does not appear to fire, even if the result shows the point was correctly determined to be outside the polygon. However, if you swipe back to the geopoint question, the constraint now appears to fire correctly and you wont be able to proceed until you pick a point inside the fence. So there seems to be a bug around firing of constraints in Collect that I need to investigate further.
Presently, this solution only works for convex polygons. In version 2 I will try to implement a more sophisticated algorithm that handles more arbitrary concave polygons. In the mean time, if you require geofencing a concave polygon, you can break up an arbitrary polygon into a set of convex ones - called polygon decomposition - and apply the above solution to each. If the target point lies within any of these convex polygons (ie OR'ed result) then it lies within the original concave polygon.
Strictly speaking, latitude and longitude are spherical coordinates, but the algorithm here treats them as cartesian (flat) coordinates. The shortest distance between two point on the glode is a geodesic path, which actually maps to a slight curve on a flat map (see https://gisgeography.com/great-circle-geodesic-line-shortest-flight-path/ for a nice visual description). On the small scale the difference is nominal, but for very large distances between fence corners it can become significant. The effect also increases the closer to the poles you get (ie higher latitudes). Additionally, the algorithm as implemented here will get 'confused' when the fence crosses the prime meridian: longitude 0. If you wish to use this in such a region, you will need to assign negative longitude values to points west of the prime meridian. I hope to address both these a bit better in version 2... ![]()
Finally, this was an interesting (and fun!) problem, which I hope it can give folks a sense of perhaps some of the more creative things you can do with XForms, in particular the ability to process lists using repeat groups! But in reality it is not a terribly efficient way to implement geofencing - it would make far more sense to accomplish this via a dedicated geofence() XPath function [something I might take a stab at someday...] The solution provided here works, but it requires imposing a distracting repeat group within your form that users must navigate thru. Although you can 'hide' repeat groups by making them irrelevant, a consequence of doing so means any embedded calculations wont be performed, alas.